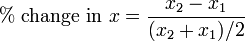For a lot of companies looking at entering the cloud computing marketplace the lack of measurable capacity metrics has become a particular problem point. Currently trying to plan future resource & capacity requirements is an extremely difficult endeavor. Recent high profile cloud outages have made the need for proactive capacity measurement painfully clear. When it comes to scaling infrastructure it seems that a lot of cloud computing has come down to a best guess mentality. (Although companies like SOASTA have done a great job at attempting to solve this problem) At the end of the day these outages are generally because of the unforeseen aspects, namely the inability to adequately determine and measure an application or infrastructure's breaking point. For this reason I believe that going forward the concept of elasticity will quickly become one of the more important aspects when designing most modern cloud centric system architectures.
To give you some background, I've been pitch my vision for elastic computing for almost 6 years. (I'm told others have also used the term before me as well) Generally my theory for Elastic Computing is in the ability to apply a quantifiable methodology that allows for the basis of an adaptive introspection with in a real time hybrid cloud centric infrastructure. But this doesn't actually address the question of "What is Elastic Computing" for that we need to dig deeper.
First we must look at what "elasticity" is and how it can be applied. According wikipedia, "in physics, elasticity is the physical property of a material when it deforms under stress (e.g. external forces), but returns to its original shape when the stress is removed. The relative amount of deformation is called the strain." Similarly elasticity applied to computing can be thought as the amount of strain an application or infrastructure can withstand while either expanding or contracting to meet the demands place on it.
One of the best examples of elasticity can be found in economics where elasticity is described as "the ratio of the percent change in one variable to the percent change in another variable. It is a tool for measuring the responsiveness of a function to changes in parameters in a relative way. A typical example is analysis of the elasticity of substitution, price and wealth. Popular in economics, elasticity is an approach used among empiricists because it is independent of units and thus simplifies data analysis."
For me, the economic centric definition is the best way to apply elasticity to cloud computing. In this approach the main benefit is the ability to measure quantifiable capacity metrics using standard mathematical formulas such as "arc elasticity" -- a formula where the elasticity of one variable is measured with respect to another between two given points. The arc elasticity method of introspection is used when there is no general function for the relationship of two variables. (Think of an unknown or sudden increase in demand placed on an application or infrastructure) Therefore this formula provides the ability of to act as a predictive estimator for required system elasticity.
Wikipedia provides this economic example.
The y arc elasticity of x is defined as:What is Elastic Computing?
where the percentage change is calculated relative to the midpoint
The quantifiable ability to manage, measure, predict and adapt responsiveness of an application based on real time demands placed on an infrastructure using a combination of local and remote computing resources.